
Energy relationships will be used to calculate the velocity: KE1+PE1=KE2+PE2 Since the 1st drop is the longest, the velocity at the bottom will be the greatest. Now it’s time to calculate the maximum velocity of the ride. That’s pretty quick for a lift hill but it is only going up one hundred feet and at a 42 degree angle. Next, use this equation to compute the time: Vf=Vo+at. How much time will it take for the train to reach the top of the lift hill? The acceleration of the train can be found using this equation: (vf)^2=(vo)^2+2ad Inserting our values: (8.04672)^2 (4.4704)^2+2(a)d Now solve for a and we get 0.45 m/s^2. One detail to note, we did not include the mass of the lift hill chain in our calculation.
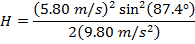
Now we know how big of a motor we will need. Substitute the KE, PE, and W equations into our energy balance equation and we get this resulting equation: Potential energy is a function of the height (PE=mgh). Kinetic energy is a function of the velocity (KE=(1/2)mv^2). Which is also written as: KE1 + PE1 + W = KE2 +PE2 Kinetic Energy + Potential Energy + Work = Kinetic Energy + Potential Energy The speed at the top of the lift will be 18mph or 8.04672 m/s.Įnergy is never destroyed, it is simply transferred from one body to another. The velocity coming out of the station will be 10mph or 4.4704 m/s. There are two other assumptions we will make at this point: the velocity of the train as it exits the station and the velocity at the top of the lift hill. We will finish calculating the force required to pull the train up the incline. This means that the train is going to be pulled up vertically a distance of 36.576m-3.048m=33.528m. We selected the angle of the lift to be at 42 degrees. Therefore, the fully loaded coaster train will have a total mass of 4500 kg (about 10,000 pounds). Each car holds two riders at 100 kg each, for a maximum mass of 735 kg (535 kg car + 2 x 100 kg riders). In order to so, we need to estimate the maximum mass of a fully loaded train to ensure our lift hill motor can pull even the heaviest train of gravy loving coaster enthusiasts up the massive hill. Let’s begin by calculating the force needed to pull the train up the lift hill incline and thus the power needed for the motor. Now, it’s time to start some calculations. There are a few basic parameters I decide to start out with: height of the station track from the ground is ten feet or 3.048 meters, height of the first hill is 120 feet or 36.576 meters, and the angle of the lift is at 42 degrees.

I plan on linking the two together later on. I will use Excel for calculations and a CAD program for drawing (though not required). Since this is my first attempt, I will make it rather simple. Please keep in mind that everything is generally simplified. Please comment if you have any questions!įirst, draw a quick sketch of the center-line of your intended layout.


 0 kommentar(er)
0 kommentar(er)
